Identifying Special Situations In Factoring

• Difference of two squares
• a²- b² = (a + b)(a - b)
• p² - 64 = p² - 8² = (p + 8)(p - 8)
• 121 - y² = 11² - y ² = (11 + y)(11- y)
• x² - 36y² = x² - (6y)² = (x + 6y)(x - 6y)
• Trinomial perfect squares
• a² + 2ab + b² = (a + b)(a + b) or (a + b)²
• x² + 6x + 9 = x² + 2(3)x + 3² = (x + 3)²
• x² - 10x +25 = x² - 2(5)x + 5² = (x - 5)² 
• x² - 5x + 25/4 = x²- 2(5/2)x + (5/2)²  = (x - 5/2)²
• a2 - 2ab + b2 = (a - b)(a - b) or (a - b) 
• 3² + 2(3)(5) + 5² =
• 7² + 2(7)(2) + 2² =
• 12² + 2(12)(9) + 9² =
• Difference of two cubes
• a³ - b³
• 3 - cube root 'em
• 2 - square 'em
• 1 - multiply and change
• 8x³ + 27 = (2x)³ + (3)³ = (2x + 3) (4x² + 6x + 9) 
•  10x³ + 30 = (4x)³ + (5)³ = (5x + 5) (6x² + 8x + 11)
•  6x³ + 25 = (x)³ + (2)³ = (2x + 4) (5x² + 4x + 10)
• Sum of two cubes
• a³ + b³ 
• 3 - cube root 'em
• 2 - square 'em
• 1 - multiply and change
•  x³ + 64 = (x + 4)(x²
•  (x + a)(x² - ax + a²)
•  (4a)³ + (1)³ = (4a + 1)(16a² - 4a + 1- 4x + 16)
• Binomial expansion
• (a + b)³ = Use the pattern
• (a + b)⁴ = 

End Behavior

Domain - x values

Range - y values referred to as f(x)

• domain → +∞, range → +∞ (rises on the right)
• domain → -∞, range → -∞ (falls on the left)

 

• domain → -∞, range → +∞ (rises on the left)
• domain → +∞, range → -∞ (falls on the right)

• domain → +∞, range → +∞ (rises on the right)
• domain → -∞, range → -∞ (falls on the left)

• domain → +∞, range → -∞ (falls on the right)
• domain → -∞, range → -∞ (falls on the left)

NAMING POYNOMIALS: 

**Degree:
0- constant

1- linear

2- quadratic

3- cubic

4- quartic

5- quintic

TERMS:                           ****Number of terms is always one less than the degree.
monomial
binomial
trinomial
quadranomial
poynomial

Quadratic Functions

THE STANDARD FORM:   ax² + bx + cy² + dy + e= 0


**You need to know the equation above to be able to tell if a graph will be an ellipse, a circle, a hyperbola, or a parabola..


*If A does not equal C and the signs are the same, then the graph is an ellipse.



*If A and C are equal, then the equation is a circle.


*If A and C are different signs then the graph is a hyperbola.



*If A and C equal 0, then the graph is a parabola.

Graphing Absolute Value Equations

**Using this Equation: y = a l x - h l +k

*Using (h, k) will help you find the vertex of the graph.

*Using the a in the equation will determine if the graph will open up or down.

*The h will tell you if it will go left or right and the k will tell you if it moves up or down

Error Analysis

Problem number 22 is wrong because the line is supposed to be dotted not solid. The shaded part is right. In problem number 23 it's wrong because the shaded part is supposed to be above the line not under. The solid line is right in this problem.





This problem is wrong because the x is going up by 5's and the y's are going up by 10's so the equation is wrong. The slope should be 2 or 10/5. Putting these numbers in the equation should be correct.




When you solve these equations you always have to plug in the numbers into each equation to make sure that the answer is corect. If you just plug it into one equation it may be right for that equation but not the other.



Number 20 is wrong because the equation says less than which means that the line is supposed to dotted not solid.


In problem 21 the equation says that y is less than or equal to. The shaded area should be underneath the line not above.

Matrix

Matrix: Rectangular array of numbers enclosed in a set of brackets.


**Dimensions of a Matrix: The number of horizontal rows it has x the number of vertical columns.

*****Dimensions = 1) Addition/Subtraction. 2) Scalar multiplication.

* Matrix multiplication is NOT commutative.

Ex:      [3 4 5 6]

      dimensions: 1 x 4

Adding Matrices:

*To add matrices, you have to add the corresponding entries (you can only add matrices of the same size)

*Row by Column

Ex: [1 2 3] + [2 1 2] = [3 3 5]
      [1 0 2]    [1 0 3]     [2 0 5]

Subtarcting Matrices:

*To subtract matrices, you have to subtract the corresponding matrices.

*Row by Column


Scalar Multiplication: If a matrix is multiplied by a scalar, each element of the matrix is multiplied by that number.

* Multiply every entry by a commen #.

*Row by Column.

Ex: 2A = [1 2 3] >        2 (1)   2 (2)   2 (3)  =
              [5 0 -1]             2        4        6      =        [2 4 6]
                                     2(5)   2(0)   2(-2)   =      [10 0 -2]
                                      10      0        -2     =
Matrix multiplication:

*Matrix mutiplication involves both multiplication and addition.

*Matrix multiplication is NOT communitive.

*Order matter: communitive property.

Ex 1: [8 6]         [-1 7] =   [-28 44 ]
    [12 10] X   [6 -2] =    [48 64]
     [-3 2]                        [15 -25]                  


Ex 2: [5 0]     [-1 7] =      5(-1) + 0(6)    5(7) + 0(-2)
      [4 7] X [6 -2] =            -5+0            35+0         
                                            -5                 35             =   [5 35]
                                     4(-1) + 7(6)    4(7) + 7(-2)   =  [40 14]
                                         -4 + 42        28 + (-14)
                                             40                14
Identity Matrix for multiplication:

* The identity matrix, I, is a matrix that has all 1's in its diagonal, & 0's everywhere else.

Ex:

The Inverse of a matrix:

* The inverse of matrix A, denoted A^-1, is a matrix such that the product of AA^-1 = I


Ex:


The determinate of a 2x2 Matrix:

* lAl = means det A = ad - bc
 A = [1 4]     6(1) - 4(3) =           -6
        [3 6]        6 - 12     =

* If det (A) = 0, the matrix does NOT have an inverse.

Systems of Equations

Inconsistent lines:

*Are parallel lines with the same slope, different Y-intercepts.

*They have No Solutions.

Ex: y = 2x + 1
      y = 2x - 4

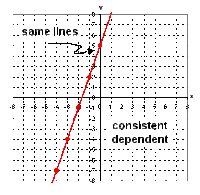
Consistent and Dependent lines:

*They are two lines overlapping one another.

*They have the same slopes, same Y-intercepts.

*These lines have All #'s

Ex: x + 2y =5
     7x + 14y = 35

Consistent and Independent lines:                                     

    

*They have different slopes.

* They have only have 1solution.

Ex: 3x + 4y = 5
      2x - 5y = 8